矢速について考える

まず、高校の物理の運動エネルギーの公式。

E=1/2*ｍ*ｖ*ｖ

E:　運動エネルギー　（単位　J　：　N-ｍ）

m:　質量　（単位　kg）

v:　速度　（単位　m/sec)　　　　

今回は、矢の発射される速度を計算してみます。　

ｖ＝（2E/m）＾0.5　　

Eは、弓から矢に与えられるエネルギー、mは矢の質量（重さ）、ｖは矢の発射速度となりますので、E,ｍを推測してｖを求めます。

矢の初速は、弓のエネルギーが2倍になれば1.4倍に、矢の質量が半分になれば1.4倍になります。

まず、矢の重さ　m：

ACE-670（6.1gr/in)　749mmとポイント110grで18g、これに、羽根、ノックを加えて約20g（0.02kg)とします。

弓が矢に与えるエネルギーは、Draw Force　Curve（引き尺とポンドの関係）を積分して、その面積から求められます。

uukha-U100XのDraw Force　Curveは、uukhaのホームページ（http://www.uukha.com/en/technologie-en.php）から、CurveをCopyし、引き尺28インチで32＃になる相似のCurveを作ってみました。

普通のDraw Force　Curveは、X軸が引き尺で単位はインチ、Y軸は弓の強さでポンドで表示されていますが、今回はこれを、X軸の単位をm、Y軸の単位をNに換算しています。

また、右側のY軸はN-m（J)の単位で、弓に蓄積されるエネルギーを示します。

青い線が、Draw Force　Curveでブレースハイトからアンカーまで引いた時の弓の力（Weight)を示しています。

アンカーでは、引き尺29.5インチで34.2ポンド（749mm-152.4N　（15.5ｋｇ）)です。

この青い線を積分して求めた弓に蓄えられるエネルギー（台形近似で求めた面積）を、赤い線で示しています。　（アンカーで44.5N-m（J)です）

弓のエネルギーは弦・リムを動かすエネルギーにも使用されますので、矢に伝わる効率を95%と想定し42.2Jを矢に伝わるエネルギーとします。

矢の重さ　　m：　20ｇ
エネルギー　E：　42.2J
から、ｖ（矢の初速）を計算すると

　　　64m/sec、232km/h　となります。（効率60％で184km/h）

私の引き尺は、29.5インチでこの初速になりますが、

28インチの場合、矢に伝わるエネルギーは、36.9Jで、初速は、60m/sec,213km/h
27インチの場合、矢に伝わるエネルギーは、33.6Jで、初速は、57m/sec,206km/h
26インチの場合、矢に伝わるエネルギーは、30.3Jで、初速は、54m/sec,196km/h　　　
　　　
と、各々7％、11%、16％ほど遅くなります。

追記：　2015/06/25
効率95%は出来過ぎのようです。

弓の効率は70％-85％ぐらいみたいです。
70％とすると、矢速は0.85倍の199km/hぐらいになります。

また、へたな撃ち方をすると、さらに効率が10％ほど落て、0.8倍の184km/hとなります。
こちらの方が実感に合っています。

2019/5/17　追記
On the Mechanics of the Arrow:Archer's Paradox 1
B.W. Kooi and J.A. Sparenberg

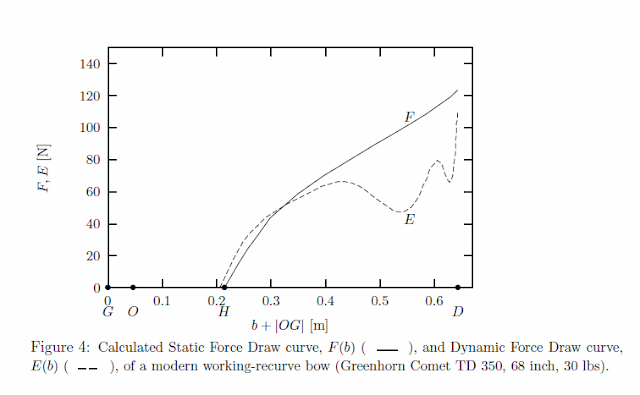
に次のForce Draw curveが提示されていました。

このカーブは、リム等の質量・戻りの速さを考慮し、弦から矢に作用する力を計算により求めてたものです。

静的なFDC（上記に書いたカーブに相当）と 動的FDC（実際に作用する力）を比較したもで、このカーブの面積の差が、効率に相当します。